Ошибка в законе Кеплера и Закон истории

Иоганн Кеплер (1571-1630 г.г.)— немецкий математик, астроном, оптик и астролог, первооткрыватель законов движения планет Солнечной системы (рис.1).
Кеплер всегда считал, что если бы не было Тихо Браге, то он не открыл бы свои законы. Тихо Браге (1546-1601г.г.) был известным датским астрономом, которому датский король Фредерик II пожаловал во владение остров Вен около Копенгагена, где Браге построил астрономическую обсерваторию Ураниборг («Небесный замок»). Большинство инструментов, которыми была оснащена обсерватория, ученый изготовил самостоятельно, поэтому при наблюдениях ему удалось добиться высокой точности измерений. Следует особо заметить, что до открытия телескопа оставалось ждать ещё несколько десятилетий, поэтому астрономические наблюдения Браге проводил невооруженным глазом. Он считал, что планеты вращаются вокруг Солнца, которое движется вокруг Земли.
Ознакомившись с работой Кеплера «Тайны мира» (1596 г.), Тихо Браге оценил хорошее знание автором астрономии, его оригинальное мышление и значительный объём выполненных вычислений. Поэтому вскоре Тихо Браге встретился с Кеплером, которому тогда было 24 года от роду, и предложил ему работу в Праге в качестве своего помощника в астрономических наблюдениях и вычислениях. Совместная работа Кеплера и Браге была кратковременной — всего около полутора лет.
После смерти Браге (1601 г.) Кеплер принимает его должность придворного астронома и астролога у императора Рудольфа II. Несмотря на высокую должность, Кеплер постоянно нуждался, потому что жалование ему платили не регулярно и не полностью, так как из-за бесконечных войн императорская казна была пуста.
Всю свою жизнь Кеплер посвятил обработке огромного объёма астрономических измерений, выполненных Тихо Браге. Уже в 1600 году Кеплер начал изучать движения Марса с целью уточнить теорию Коперника, который считал, что планеты вращаются вокруг Солнца по окружностям. Предпочтение Марсу в изучении движения планет Кеплер отдал потому, что именно в видимом движении Марса обнаруживались наибольшие отклонения от равномерного движения по кругу.
Вначале Кеплер разделял традиционное убеждение, что небесные тела могут двигаться только по кругам, и поэтому он потратил много времени на то, чтобы подобрать для Марса круговую орбиту. После многолетних и очень трудоёмких вычислений, отказавшись от общего заблуждения о кругообразности движений, Кеплер предпринимает попытки проверить свои формулы на кривой овала, затем на кривой яйцеобразного овала. Продолжая размышления и расчёты, он писал в 1604 году: «Правда лежит между кругом и овалом, как будто орбита Марса есть точный эллипс». Наконец, в 1605 г. он проверил вариант эллипса, и всё сошлось в его расчетах.
В 1609 году в Праге вышла из печати книга Кеплера «Новая астрономия». В этой книге Кеплер излагает свои два эмпирических закона. Первый закон гласил: «Планеты обращаются вокруг Солнца по эллиптическим орбитам, при этом Солнце располагается не в центре эллипса, а в одном из фокусов эллипса. Следовательно, расстояние планеты от Солнца не всегда одинаковое (закон эллипсов)».
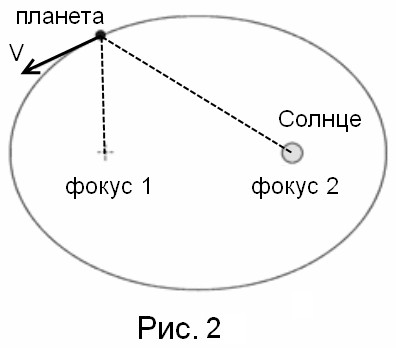
Эллипсом называется кривая, являющаяся геометрическим местом точек, для каждой из которых сумма расстояний от неё до двух фиксированных фокусов постоянна (рис. 2). В данном определении эллипса содержится способ его получения. Если вбить два гвоздя и соединить их нитью, длина которой больше расстояния между гвоздями, то карандаш, натягивающий нить, начертит эллипс относительно двух гвоздей. Связав эти фиксированные точки эллипса с Солнцем, именно Кеплер дал им название «фокус», что означает «очаг».
Кеплер стал автором первого обширного (в трёх томах) изложения коперниканской астрономии, которое немедленно удостоилось чести попасть по решению инквизиции в «Индекс запрещённых книг», но именно в эту книгу, свой главный труд, Кеплер включил описание всех своих открытий в астрономии.
Альберт Эйнштейн назвал Кеплера «несравненным человеком» и писал о его судьбе так: «Он жил в эпоху, когда ещё не было уверенности в существовании некоторой общей закономерности для всех явлений природы. Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и не понятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения!».
В 1630 году Кеплер умер в нищете. Со смертью Кеплера его злоключения не закончились. В конце Тридцатилетней войны было полностью разрушено кладбище, где он был похоронен, и от его могилы ничего не осталось. Только в 1808 году, почти через 200 лет после смерти, ему был поставлен памятник.
Не все учёные, современники Кеплера, восприняли его законы движения планет, например, Галилей не признавал факт неравномерного движения планет. Ведь движение по инерции не может быть неравномерным! Лучше уж пусть будут круги в виде деферентов и эпициклов Птолемея, чем неправильный эллипс.

Попытку найти математическое выражение кривой, которая более точно соответствовала бы фактической траектории планет, сделал в 1680 году Джованни Кассини (рис.3).
Джованни Доменико Кассини (1625-1712 г.г.), итальянец, учился в Генуе и в 1650 году стал профессором математики и астрономии в Болонском университете. Затем он был вызван в Рим, где продолжил астрономические работы. Слава Кассини, как астронома, была так велика, что в 1669 г. он был избран членом Парижской академии наук, и король Людовик XIV пригласил его занять пост директора Парижской обсерватории, которую он возглавлял до конца своей жизни.
В 1680 году Кассини изучал кривую кассиниану (овал Кассини), которая является сечением тора и представляет собой геометрическое местом точек, для каждой из которых произведение расстояний от двух фиксированных фокусов постоянно. Он работал над этой кривой в процессе изучения относительных движений Земли и Солнца и предложил, что она, как кривая для планетарных орбит, подходит больше, чем предложенный Кеплером эллипс.
В том случае, если изменение длины радиуса орбиты планеты является малым (у орбиты Марса полуоси эллипса отличаются на 1/11 часть, у орбиты Земли – на 1/65), то линии эллипса и овала Кассини практически совпадают. Кто же всё-таки прав: Кеплер или Кассини? По каким орбитам движутся планеты: по «эллипсам Кеплера» или по «овалам Кассини»?
Известно, что Ньютон вывел свои законы механики и закон Всемирного тяготения, используя законы Кеплера. Если считать первый закон Кеплера ошибочным, то придётся пересмотреть законы Ньютона, которые считаются незыблемыми.
Поэтому сейчас общепринято, что Кассини придерживался устарелых физических концепций, а именно: был противником теории всемирного тяготения и предлагал заменить эллипсы Кеплера кривыми четвертого порядка (овалами Кассини).
После Кеплера, благодаря усилиям многих поколений учёных, были созданы новые методы исследования и описания движения планет в Солнечной системе. Оказалось, что законы Кеплера только лишь приближённо соответствуют реальному движению планет. Для объяснения этого факта считается, что законы строго выполнялись бы, если бы в пространстве существовали только два изолированных тела — Солнце и планета. В таких условиях орбита планеты являлась бы точным эллипсом и называлась бы невозмущённой или Кеплеровой орбитой. Однако в Солнечной системе много планет, которые по закону Всемирного тяготения взаимодействуют не только с Солнцем, но и между собой, отклоняя свои реальные орбиты от идеальных траекторий. Отклонения планет от движения по эллипсам называются возмущениями.
В настоящее время, путём подбора параметров Солнца и планет, создана такая структура Солнечной системы, которая теоретически объясняет деформацию идеальных Кеплеровых орбит воздействием планет друг на друга. Поэтому сейчас трудно сделать вывод о том, что именно заставляет планеты отклоняться от закона Кеплера: возмущения со стороны других планет или ошибка в формулировке первого закона (закона эллипсов).
Необходимость поиска закономерностей, определяющих фактические траектории небесных тел в Солнечной системе, вытекает не только из наличия отклонения планет от Кеплеровых орбит.
Например, наблюдая за движением астероидов, ученые из США и Чешской республики впервые сумели зарегистрировать еле заметную, но теоретически очень важную силу негравитационного происхождения, действующую на все небесные тела в Солнечной системе (статья «Обнаружена загадочная сила, подталкивающая астероиды к Земле»). Фактически, были обнаружены систематические отклонения траекторий астероидов от пути, предписанного им законом Всемирного тяготения и законами Кеплера. Для объяснения этих отклонений невозможно произвольно изменять значение массы астероида, который имеет конкретные размеры и плотность, поэтому потребовалось найти дополнительную возмущающую силу. В качестве источника такой силы обычно рассматривается эффект Ярковского, ставший важным инструментом для описания многих аспектов динамики астероидов.
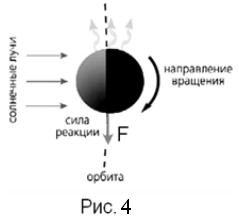
И.О.Ярковский, пытаясь в 1900 году объяснить вечное движение планет вокруг Солнца через эфир, который должен оказывать сопротивление этому движению, предположил, что вечное движение планеты обеспечивает тепловая машина, источником тепла для которой является Солнце. По мнению Ярковского, планета поглощает окружающий эфир, который в её недрах частично превращается в химические элементы, а частично – покидает планету. Чем выше температура поверхности планеты в каком-либо её месте, тем интенсивнее частицы эфира устремляются наружу создавая эффект отдачи. На рис.4, взятом из статьи В.Г.Сурдина «Эффект инженера Ярковского», показано, что вращаясь, планета переносит наиболее нагретый участок поверхности на вечернюю сторону, где эфир выделяется и создаёт силу, преодолевающую сопротивление эфира движению планеты по орбите.
Сегодня в науке нет места эфиру в пустом космическом пространстве, но есть давление и отражение света, которое теоретически может создавать силу, подобную эффекту Ярковского. Введение такой теоретической силы позволяет объяснить отклонение фактических траекторий малых космических объектов, в том числе, астероидов и искусственных спутников Земли, от их теоретического положения.
Таким образом, и большие и малые космические объекты требуют введения различных возмущающих сил для объяснения различий между теорией и практикой. Поэтому у нас имеются веские основания для проведения критического анализа сущности первого закона Кеплера.
Дополнительным оправданием наших сомнений в справедливости первого закона Кеплера является его явная неопределённость, которая состоит в том, что если в одном фокусе эллипса находится Солнце, то, что тогда должно находиться в его втором фокусе? Чем один фокус хуже другого? Было бы гораздо понятнее, если бы кривая, которая определяет траекторию планет, содержала бы только одно место для Солнца.
Как мы увидим далее, такой кривой является именно эллипс, но Солнце не должно находиться в его фокусе. Тогда в какой же точке эллипса находится Солнце? В чём состоит ошибка Кеплера?
Кеплер взял фокус эллипса за центр Солнца, так как математический эллипс не содержит других характерных точек, смещённых от его центра.
Ошибка в первом законе Кеплера вызвана тем, что за две тысячи лет существования теории конических сечений, у самих конических сечений так и не был выявлен их главный характерный параметр, что позволило считать эллиптические сечения конуса и цилиндра абсолютно идентичными. Мы же будем называть их более конкретно – коническим и цилиндрическим эллипсом, так как они принципиально отличаются друг от друга.
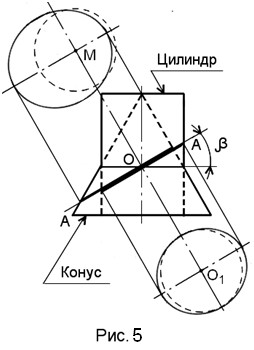
Это наглядно можно увидеть, если одновременно построить два эллипса, являющихся сечением конуса и цилиндра. На рис.5 показаны конус и цилиндр, оси которых совпадают, а поверхности пересекаются по окружности с центром О, которую мы назовём «исходной». Проведём через исходную окружность горизонтальную секущую плоскость и повернём её вместе с исходной окружностью относительно центра О на угол ? в положение А-А.
Ниже секущей плоскости А-А, в проекционной связи, показано сечение цилиндра, которое представляет собой привычный нам цилиндрический эллипс с единственной характерной точкой О1, которая является проекцией точки О и геометрическим центром эллипса. Такой эллипс можно получить пропорциональным математическим «растяжением» исходной окружности, проекция которой показана пунктиром. «Растяжение» вдоль большей оси эллипса обеспечивается умножением координат всех точек исходной окружности вдоль данной оси на коэффициент, величина которого больше единицы.
Выше секущей плоскости А-А показано эллиптическое сечение конуса, которое расположено явно несимметрично относительно проекции центра О исходной окружности — точки М, так как конический эллипс с одной стороны очень растянут относительно исходной окружности, а с другой, наоборот, сжат. Таким образом, конический эллипс на рис.5 имеет тоже всего лишь одну характерную точку М, которая не совпадает с геометрическим центром эллипса и представляет собой проекцию точки О, то есть точки пересечения оси конуса с секущей плоскостью, порождающей данный эллипс. В дальнейшем, для упрощения описания точки М конического эллипса, мы будем называть её «мюп-центром». Это явное отличие эллипса конического от эллипса цилиндрического влечёт за собой далеко идущие последствия. Однако это отличие не нашло места в геометрии, в которой существует только симметричный цилиндрический эллипс. Почему это произошло?
Во-первых, геометрия изучает конические сечения только как математические кривые, стараясь придать их уравнениям самый простой вид. Это возможно только тогда, когда уравнения имеют каноническую форму, достигаемую при симметричном расположении изучаемого конического сечения относительно осей координат. Действительно, если на рис.5 верхнее коническое сечение расположить симметрично осям координат, сдвинув точку М в геометрический центр эллипса, то мы получим полное подобие конического и цилиндрического эллипса.
Во-вторых, с помощью сфер Данделена геометрия наглядно выявила геометрические свойства эллипсов — фокальное, директориальное, оптическое, которые оказались одинаковыми, как для цилиндрических, так и для конических эллипсов, что ещё более способствовало исключению «мюп-центра» из числа характерных параметров конического эллипса. Одновременно, этот параметр исчез из характерных точек остальных конических сечений – гипербол и парабол.
Однако то, что является несущественным для геометрии конических сечений, оказалось существенным для небесной механики, которая, с подачи геометрии, вместо основного (первичного) параметра конических сечений (мюп-центра) использовала вторичный параметр – один из двух фокусов.
Поэтому имеет смысл наглядно показать во всех конических сечениях положение «мюп-центра», в котором должно находиться Солнце.
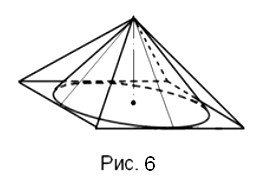
Если взять конус и продолжить его образующие вверх, то мы получим полный конус, который представляет собой две конические половинки (полы), вершины которых стыкуются друг с другом. Теперь, если взять одну половину (полу) конуса с углом 900 при его вершине и поместить её внутрь равносторонней четырёхгранной пирамиды, боковые плоскости которой касаются поверхности конуса, то мы получим фигуру, изображённую на рис.6.
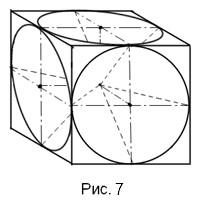
Из шести таких фигур можно собрать куб, показанный на рис.7. Внутри такого куба противоположные полы конусов образуют три полных конуса, вершины которых находятся в центре куба, а боковые поверхности касаются друг друга. Плоские поверхности пирамид тоже касаются друг друга, образуя вокруг каждого конуса пространство, которое можно считать областью существования конуса.
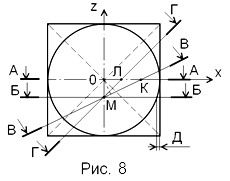
Если мы совместим центр такого куба и оси конических поверхностей с началом и осями декартовой (прямоугольной) системы координат, то, проводя различные секущие плоскости, мы можем увидеть взаимодействие конических сечений друг с другом. На рис.8 показаны положения секущих плоскостей, сечение которых мы будем рассматривать.
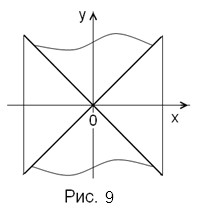
На рис.9 показано горизонтальное сечение куба плоскостью А-А, проходящей через начало системы координат О и оси двух горизонтальных конусов. В данном сечении мы видим только две пересекающиеся прямые линии, которые проходят под углом 450 к осям координат. Эти линии представляют собой линии пересечения секущей плоскости с двумя горизонтальными конусами (из двух пол) и их пирамидами, но так как в плоскости А-А конусы и их пирамиды касаются друг друга, то в сечении образуется одна линия, являющаяся линией их соприкосновения.

На рис.10 показано горизонтальное сечение куба плоскостью Б-Б, которая расположена ниже плоскости А-А, параллельна осям X, Z и перпендикулярно пересекает ось Y. Плоскость Б-Б рассекает все три конуса и образует сечения (конические), показанные сплошными толстыми линиями – окружность и две сопрягающиеся равнобочные гиперболы, каждая из которых состоит из двух ветвей. Эти сечения являются каноническими, так как они симметричны осям координат, при этом геометрические центры О таких конических сечений всегда совпадают с их «мюп-центром», то есть с точкой пересечения горизонтальной секущей плоскости с вертикальной осью координат. Пересечения секущей плоскости с пирамидами показаны прерывистыми толстыми линиями, которые образуют зоны существования сечений. Основой этих зон является квадрат, который называется «фундаментальным».
Областью существования окружности является фундаментальный квадрат, в который она вписана. Считается, что гиперболы вневписаны в фундаментальный квадрат, так как областью их существования является зона вне квадрата, ограниченная продолжениями двух пересекающихся диагоналей «фундаментального квадрата». Эти продолжения называются асимптотами и совпадают с сечением пирамид.
В каноническом виде сечений мы можем выделить на рис. 10 следующие характерные точки.
Точка О указана вместо точки М (на рис.8), так как она является геометрическим центром канонических сечений. Если мы опишем пунктиром окружность относительно фундаментального квадрата на рис.10, то точки её пересечения с осями координат (точки 1,2,3,4) являются фокусами гипербол, а если мы впишем тонкими линиями квадрат в центральную окружность, то стороны этого квадрата являются директрисами соответствующих ветвей гипербол. Эти директрисы пересекают оси координат в точках 5,6,7,8, которые можно назвать фокусными точками окружности. Тогда точки 1,2,3,4 можно назвать директрисными точками окружности (смотри окружность Аполлония). Так как окружность симметрична относительно центра О, то её фокусные и директрисные точки образуют концентрические окружности и для исходной окружности обычно не выделяются.
Таким образом, для сопряжённых по фундаментальному квадрату (примыкающих друг к другу) конических сечений фокусы одного сечения находятся на директрисах другого.
Это свойство сохраняется даже при изменении формы канонических сечений путём их аффинного преобразования – деформации пропорциональным математическим «растяжением». На рис.11 показана форма, которую приобретут горизонтальная гипербола и окружность, если координату каждой их точки по оси Х умножить на коэффициент, больший единицы.
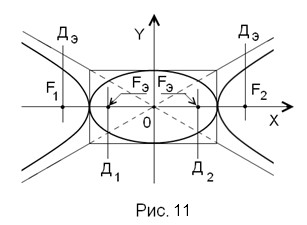
Мы видим, что на рис.11 сечения остались каноническими, то есть симметричными осям координат, но фундаментальный квадрат стал фундаментальным прямоугольником, окружность – цилиндрическим эллипсом, а гипербола стала неравнобочной, так как асимптоты стали продолжением диагоналей прямоугольника, а не квадрата. Точки 1,3,5,7 (рис.10) превратились на рис.11 в фокусные и директориальные точки цилиндрического эллипса и гиперболы.
Термин «асимптота» был введён Аполлонием Пергским для канонического сечения и означает «несливающаяся» с гиперболой. Действительно, на рис.8 в сечении Б-Б существует зазор Д между поверхностью конуса и пирамиды. Если продолжать конус и пирамиду в бесконечность, то этот зазор будет уменьшаться, но он всегда будет существовать. Это стало до того привычным, что даже в учебниках это свойство трактуется как фундаментальное свойство гиперболы.
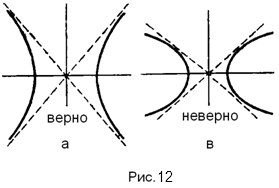
Например, на рис.12 приведён рисунок из учебника А.Д. Александрова «Геометрия», на котором показано, как верно и как неверно изображать гиперболу относительно асимптот. На рисунке показано, что если гипербола касается асимптоты, то это является ошибкой. Однако в реальной жизни всё может быть совершенно иначе, так как каноническая форма гиперболы является всего лишь единичным случаем из множества возможных положений гиперболы (конического сечения) относительно осей координат (осей конусов).
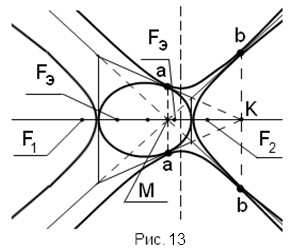
Давайте рассмотрим на рис.13 сечение В-В, полученное на рис.8 поворотом секущей плоскости Б-Б относительно точки М в положение В-В. При этом секущая плоскость В-В параллельна оси У и не перпендикулярна осям Х и Z. Сплошными толстыми линиями на рис.13 показаны сечения трёх конусов, а сплошными тонкими линиями — сечения пирамид, определяющих прежние асимптоты — область существования соответствующих конических сечений.
Как видите, в реальном коническом сечении фундаментальный квадрат превратился не в прямоугольник, а в трапецию, диагонали которой стали не асимптотами (несливающимися), а касательными к гиперболам, которые сливаются вместе в точках касания «b». Точка М (мюп-центр эллипса) лежит на пересечении диагоналей фундаментальной трапеции и является точкой пересечения секущей плоскости В-В с осью Z. На пересечении (продолжении) боковых сторон трапеции лежит точка К (мюп-центр горизонтальной гиперболы) – точка пересечения секущей плоскости В-В с осью Х (см. рис.8).
Через мюп-центр эллипса (точку М) проведена пунктиром вертикальная прямая «а-а», соединяющая точки «a», которые являются точками касания эллипса с сопряжённой (примыкающей) вертикальной гиперболой и боковыми сторонами трапеции. Через мюп-центр гиперболы (точку К) проведена пунктиром вертикальная прямая «b-b», соединяющая точки «b», которые являются точками касания гипербол. Продольная ось вертикальной гиперболы является проекцией оси У, на которой находится вершина конусов (точка О на рис.8). У эллипса и горизонтальной гиперболы показаны фокусы и геометрический центр, которые не совпадают с мюп-центрами М и К.
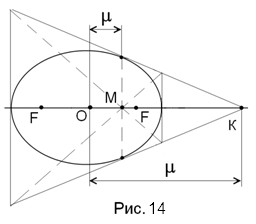
На рис.14 показано увеличенное изображение конического эллипса с рис.13, из которого видно, что мюп-центр М смещён относительно геометрического центра эллипса О на величину µ, которую будет удобно называть мюп-эксцентриситетом. Мюп-центр К гиперболы тоже смещён относительно геометрического центра О гиперболы на аналогичный мюп-эксцентриситет.
Таким образом, в математике существуют только канонические формы конических сечений, которые представляют собой только два предельных положения секущей плоскости: перпендикулярное и параллельное к оси конуса. Только в этом случае диагонали «фундаментального» четырёхугольника становятся асимптотами, так как точка контакта конического сечения с диагоналями смещена в бесконечность. Все остальные положения секущей плоскости превращают асимптоты в касательные линии к коническим сечениям и дают мюп-центр, который лежит на линии, соединяющей точки касания.
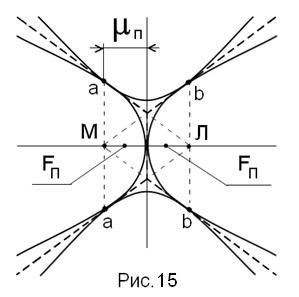
Для того чтобы найти положение мюп-центра в параболе, давайте рассмотрим на рис. 15 сечение Г-Г, которое повёрнуто относительно точки М так, что секущая плоскость проходит параллельно ближайшей к ней образующей вертикального и горизонтального конуса на рис.8.
Толстыми пунктирными линиями изображены линии пересечения секущей плоскости Г-Г с пирамидами трёх конусов. Для данного сечения характерным является то, что левое (большое) основание фундаментальной трапеции (см. рис.13), вместе с точкой контакта левой ветви горизонтальной гиперболы и левой части эллипса, переместилось влево и исчезло на рис.15 за счёт перемещения геометрического центра О эллипса и гиперболы в бесконечность.
Таким образом, бывший эллипс и бывшая гипербола, потеряв свои левые половины, уже перестали быть эллипсом и гиперболой, а превратились в две симметричные кривые, называемые параболами с фокусами Fп, при этом:
1) точка М и линия «а-а» левой параболы не изменили своего расположения в пространстве, так как секущая плоскость поворачивалась в положение Г-Г относительно неподвижной точки М;
2) ось вертикальной гиперболы совместилась с точкой касания парабол (с меньшим основанием бывшей «фундаментальной трапеции»);
3) точка К с линией «b-b» правой параболы заняла положение точки Л и стала симметричной точке М и линии «а-а» левой параболы (см. рис.8).
Обычно для параболы область её существования не определяется, так как никогда не определяется её мюп-центр, но на рис.15 видно, что областью существования левой параболы (бывшего эллипса) является пространство, ограниченное малым основанием бывшей фундаментальной трапеции и её боковыми сторонами, которые касаются точек «а» и пересекаются в мюп-центре Л сопрягаемой правой параболы. Областью существования правой параболы является пространство, ограниченное малым основанием и диагоналями бывшей трапеции, касающимися точек «б» и пересекающимися в «мюп-центре» М сопрягаемой левой параболы. При этом диагонали бывшей фундаментальной трапеции стали параллельными её боковым сторонам вследствие перемещения большого основания трапеции в бесконечность.
Таким образом, диагонали и боковые стороны бывшей фундаментальной трапеции стали параллельными друг другу и симметричными относительно точки контакта сопряжённых парабол, проходя через симметричные мюп-центры.
Разрушение фундаментального четырёхугольника на рис.15 и потеря второго фокуса бывшей гиперболой и эллипсом, говорит нам о том, что только мюп-центры конических сечений являются их основными характеристическими точками, которые пока отсутствуют в теории конических сечений. Так как геометрический центр параболы находится в бесконечности, то целесообразно считать мюп-эксцентриситетом параболы (µп) расстояние от её мюп-центра до плоскости симметрии сопрягаемых парабол на рис.15.
Сегодня считается, что парабола – это одна разомкнутая кривая, гипербола – две разомкнутые ветви одной кривой, эллипс – одна замкнутая кривая.
В связи с тем, что парабола, как мы выяснили, представляет собой половину эллипса или половину гиперболы, то логично пересмотреть существующее понятие об эллипсе. Очевидно, что эллипс – это две замкнутые ветви одной кривой. Отличие эллипса от гиперболы состоит в том, что две его ветви имеют одну и ту же область существования в виде фундаментального четырёхугольника и смыкаются внутри него, хотя каждая из ветвей тоже имеет свой фокус, как и ветви гиперболы.
Если параболы, гиперболы и эллипсы имеют разное количество ветвей и фокусов, то любое коническое сечение имеет только один мюп-центр, который является первородной точкой конического сечения, то есть точкой пересечения оси исходного конуса с секущей плоскостью, рождающей данное сечение.
Если Кеплер искал в эллипсе точку, смещённую от центра эллипса, то единственный мюп-центр находится между фокусом и центром эллипса и снимает вопрос о втором пустом фокусе эллипса. С учётом этого можно переформулировать первый закон Кеплера следующим образом: «Планеты обращаются вокруг Солнца по эллиптическим орбитам, при этом Солнце располагается не в центре, а в мюп-центре эллипса. Следовательно, расстояние планеты от Солнца не всегда одинаковое (закон эллипсов)».
Для любого эллипса можно построить только один исходный цилиндр, если считать эллипс цилиндрическим, и только один исходный конус, если считать эллипс коническим. Только конический эллипс даёт положение мюп-центра, в котором находится Солнце. То же самое можно сказать и о других конических сечениях.
Тогда объединённый первый закон Кеплера можно сформулировать в следующем виде: «Орбиты небесных тел имеют форму конических сечений, в мюп-центре которых находится иное небесное тело».
Уточнить первый закон Кеплера необходимо для обеспечения безопасности цивилизации на Земле, которой угрожают космические странники – астероиды и кометы. Сегодня считается, что какие-то неведомые силы, типа сил от эффекта Ярковского, изгибают их траекторию в сторону Земли. Предсказать эти изменения, практически, невозможно, но ориентировочно подсчитано, что, например, астероид Апофиз может столкнуться с Землёй в 2036 году.
Только внесение уточнений в теорию движения Земли, астероидов и искусственных спутников Земли, даст астрономам возможность делать более точные прогнозы о космической угрозе жизни человечества.
Submitted by ©Ю.П. Мягких, 2015
